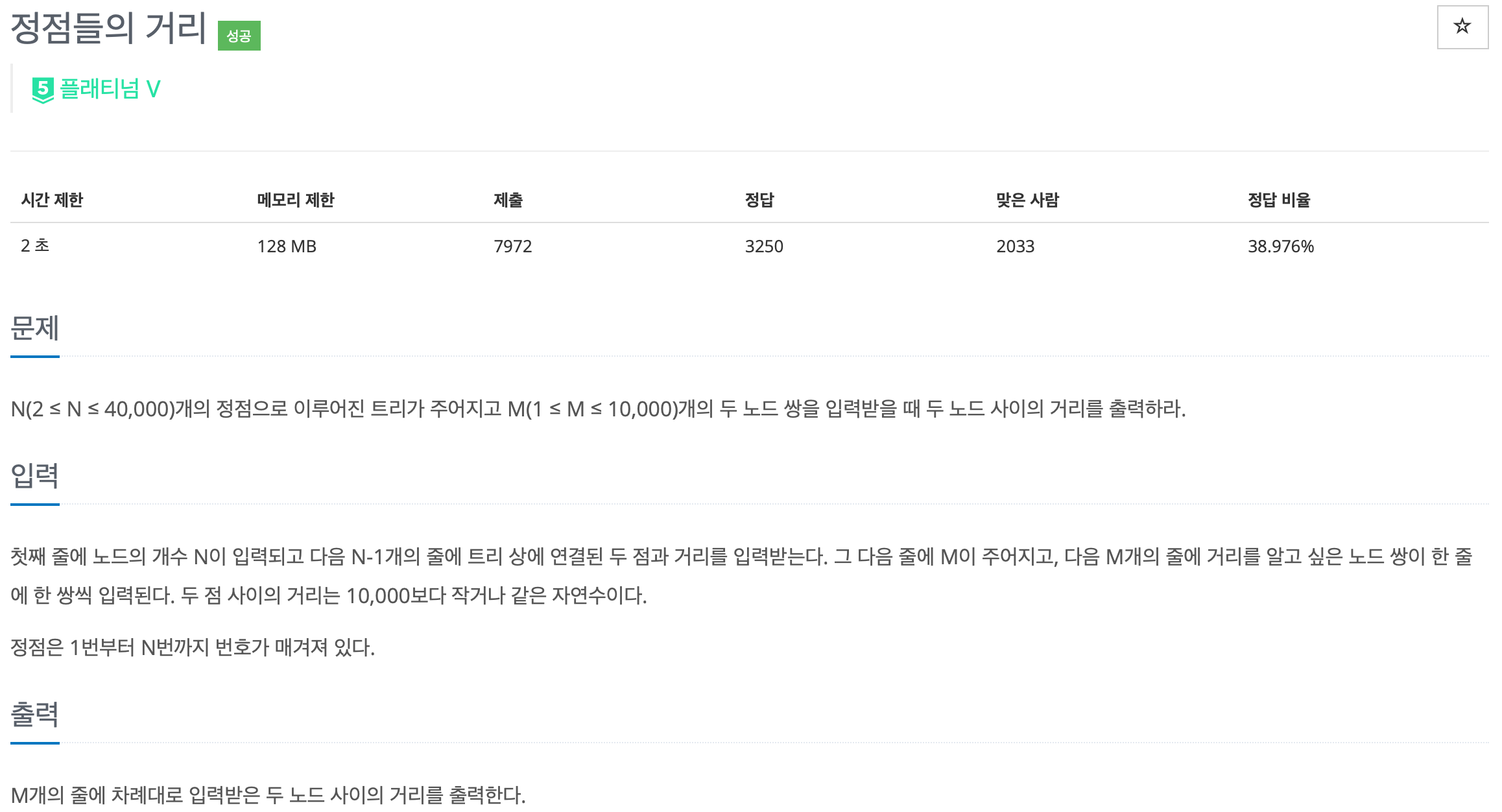
LCA를 활용하는 문제이다. LCA 분류 문제만 풀다보니 거의 같은 코드에 조금만 바꾸는 느낌이 계속 든다.
근데 LCA 알고리즘은 진짜 신기한것 같다. 관련 포스팅을 몇개 연속해서 써도 얘가 돌아가는 매커니즘이 계속 신기하다. 2진수 사고방식을 쉽게 머리속에서 굴릴 수 있는 사람이 처음 만든 것 같은데, 어쩜 저런 생각을 했는지...
각설하고. 이번 문제는 이전에 있었던 도로 네트워크 와 거의 유사하다. 중간중간 코드 몇줄만 바꿀정도. LCA에 대한 개념부터 보고싶다면 LCA 설명 글도 있다.
도로 네트워크에서는 parents[] 배열 이외에 pathMax[K][V], pathMin[K][V] 배열이 존재해 각각 2^K 번째 노드까지 경로 중 cost가 최소인 것과 최대인 것을 저장했었다.
이 문제에서는 경로에서 만나는 cost의 최소/최대값을 구하는것이 아니라 경로에 포함된 에지 cost의 합을 구하면 된다.
따라서, pathMax, pathMin 배열 대신 dist[K][V] 배열을 만들어, V에서부터 2^K 번째 조상 노드까지의 경로 cost 합을 저장하게 된다.
이 배열 값의 조합으로 우리는 특정된 두 노드에서부터 LCA가지의 경로 Cost 합을 계산할 수 있고, 그 두개의 합이 두 노드를 잇는 최단 거리이다.
#include <iostream>
#include <vector>
#include <string.h>
#define MAX_H 16
int parents[MAX_H][40000];
int dist[MAX_H][40000];
int depth[40000];
void initTree(int node, std::vector<std::pair<int, int> > adj[])
{
for (int i = 0; i < adj[node].size() ; i++)
{
int next = adj[node][i].first;
int nextDist = adj[node][i].second;
if (depth[next] == -1)
{
parents[0][next] = node;
dist[0][next] = nextDist;
depth[next] = depth[node] + 1;
initTree(next, adj);
}
}
}
int main()
{
std::ios::sync_with_stdio(0);
std::cin.tie(0);
std::cout.tie(0);
int N;
std::cin >> N;
std::vector<std::pair<int, int> > adj[N];
for (int i = 0; i < N - 1 ; i++)
{
int a, b, c;
std::cin >> a >> b >>c;
a--;
b--;
adj[a].push_back(std::pair<int, int>(b, c));
adj[b].push_back(std::pair<int, int>(a, c));
}
memset(parents, -1, sizeof(parents));
std::fill(depth, depth + N, -1);
depth[0] = 0;
initTree(0, adj);
for (int K = 0; K < MAX_H - 1; K++)
{
for (int V = 1; V < N; V++)
{
if (parents[K][V] != -1)
{
parents[K+1][V] = parents[K][parents[K][V]];
dist[K+1][V] = dist[K][V] + dist[K][parents[K][V]];
}
}
}
int M;
std::cin >> M;
for (int c = 0; c < M; c++)
{
int u, v;
std::cin >> u >> v;
u--;
v--;
if (depth[u] < depth[v])
std::swap(u, v);
int diff = depth[u] - depth[v];
int uDist = 0;
int vDist = 0;
for (int i = 0; diff; i++)
{
if (diff % 2)
{
uDist += dist[i][u];
u = parents[i][u];
}
diff /= 2;
}
if (u != v)
{
for (int K = MAX_H - 1; K >= 0; K--) // K는 max_h -1 부터 시작해야 -> outofbounds
{
if (parents[K][u] != -1 && parents[K][u] != parents[K][v])
{
uDist += dist[K][u];
vDist += dist[K][v];
u = parents[K][u];
v = parents[K][v];
}
}
uDist += dist[0][u];
vDist += dist[0][v];
}
std::cout << uDist + vDist << '\n';
}
}코드를 보면, parents[] 배열의 값을 수정하거나 참조할 때, dist[] 배열도 같이 접근한다는 것을 볼 수 있다.
parents[] 배열의 값을 넣으면서, 그 관계에 있는 두 노드의 거리를 dist[]에서도 저장하게 된다.
parents[] 배열을 탐색하면서 LCA 를 찾아갈때도, u와 v가 바뀔 때 거리를 저장한다.
마지막 탐색이 끝난 뒤, 역시 u와 v는 LCA 바로 밑 갈라진 상태이므로, LCA 까지의 거리를 합하여 두 노드에서 LCA까지 총 거리를 각각 구할 수 있다.
이것을 합하면! 짜잔... 두 노드 간 최소거리!
역시 LCA는 신기하다...
오늘도 평온한 하루가 되길. 슨민.
'짜잘한 기록' 카테고리의 다른 글
| 백준 1626 두 번째로 작은 스패닝 트리 (0) | 2021.09.06 |
|---|---|
| 백준 15481 그래프와 MST (0) | 2021.09.04 |
| 백준 3176 도로 네트워크 (0) | 2021.09.02 |
| 백준 11438 LCA 2 (0) | 2021.09.02 |
| [나만 몰랐던 알고리즘] MST 구하기 - Kruskal's Algorithm (0) | 2021.09.01 |



